Login with Magic Link?
-
Sorry, I was moving quick last night and misunderstood your comment. What do you mean you can't edit the redirect? Can you share a screenshot, please?
-
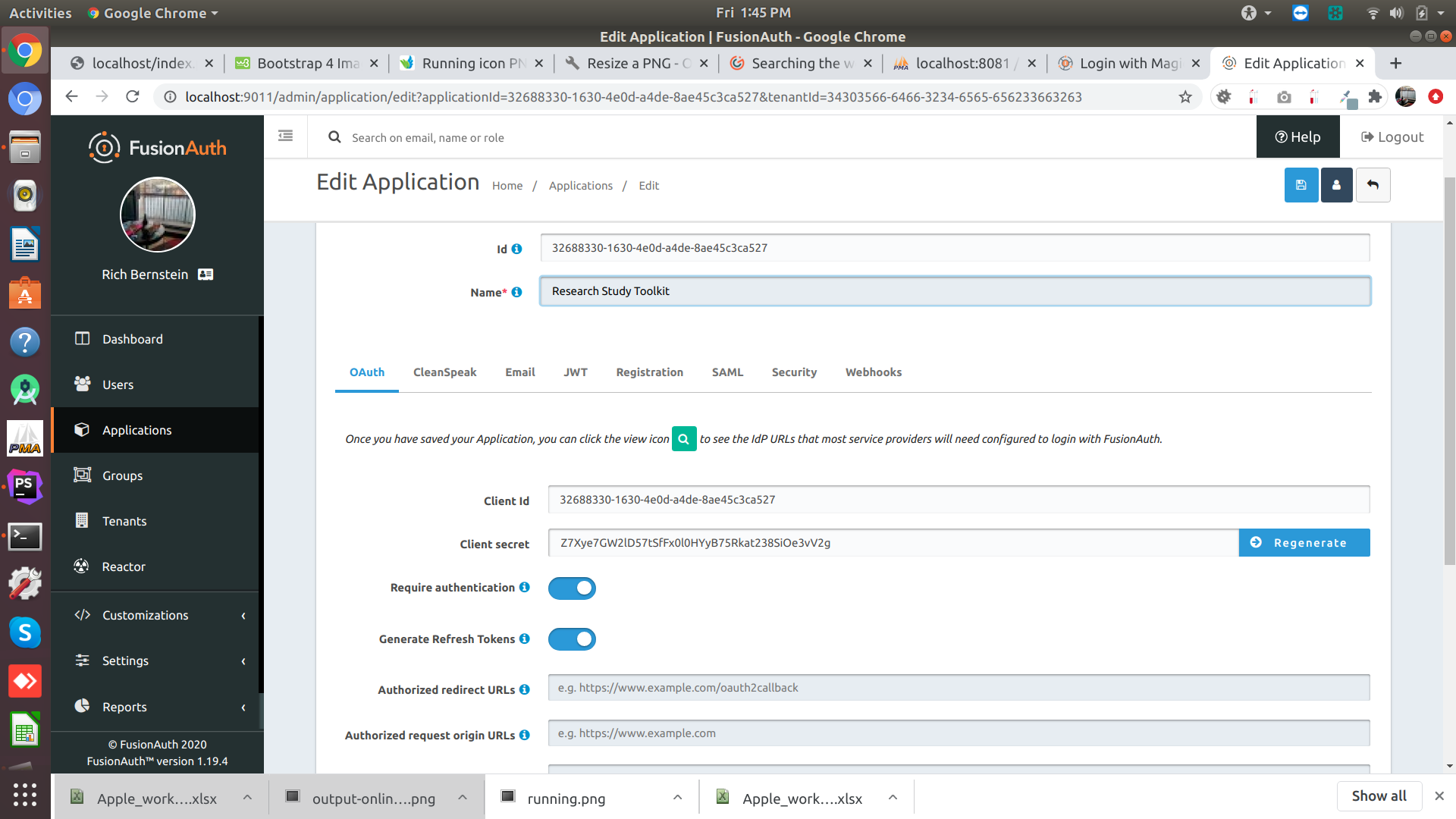
see the very bottom? Authorized redirect URLs? I can't seem to change that since it is greyed out.
-
Ah, that's a ux quirk. It isn't actually disabled, you should be able to add one or more urls to it.
You can see how I add a redirect url here: https://youtu.be/trzY5otEgKM?t=254
Hope that helps.
-
Thanks Dan. I watched the video. No, it will not take my redirect URL. Now, I don't have https on my laptop. Is that the issue? I am developing in a docker container on the laptop.
-
You can't paste text into that input box, you have to type it. Are you trying to paste it in, perhaps?
If not, then there's something I don't understand going on.
Developing in docker shouldn't affect this.
Are you logged in as the admin user?
-
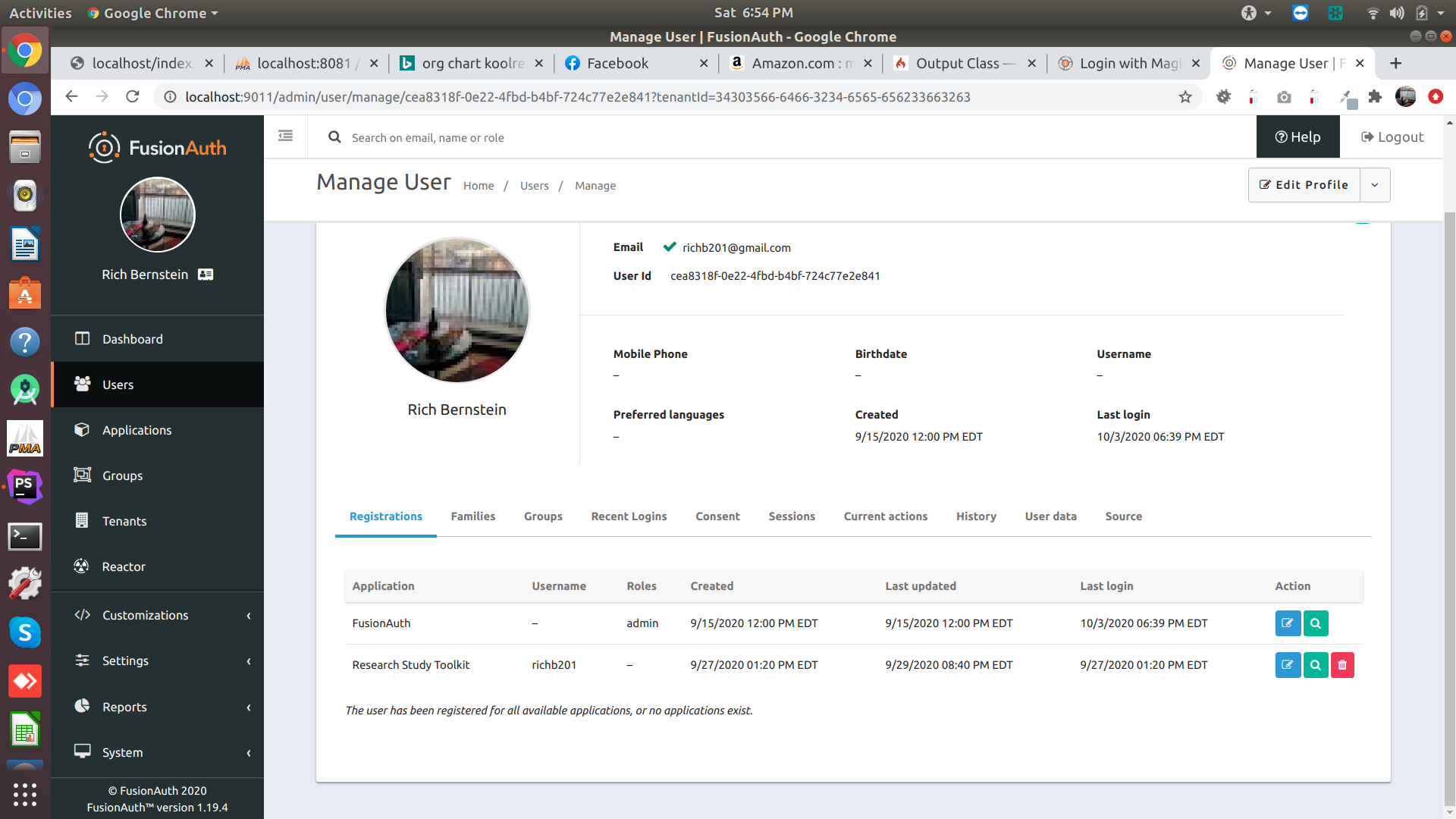
I am logged in as me and looking at the Users (attached) I am NOT an admin. Must I change that and how? BTW, my shirt came today. TY.
BTW, what does cat /etc/password mean?
-
Hiya,
You are an admin (you have the admin role in the FusionAuth app) so you should be able to add a redirect URI.
Any chance you can record and upload a video of you trying to add the redirect URI? Everything looks solid from what I can see, so I'm a bit confused about what is happening.
Glad you got the shirt!
cat /etc/passwdis unix-speak for "show my all your passwords"
-
@dan said in Login with Magic Link?:
You can't paste text into that input box, you have to type it. Are you trying to paste it in, perhaps?
I was wrong, you can paste it in. You just can't paste in two or more urls.
-
@dan said in Login with Magic Link?:
You are an admin (you have the admin role in the FusionAuth app) so you should be able to add a redirect URI.
But I am trying to use the Research Credit Toolkit application. I haven't tried it with the FusionAuth application yet. Anyway I am going to try to record a screen video. I use Screenshot which doesn't have that ability. Can you recommend an app to do the recording with?
-
Notice that when I first login to the control panel (see attached), the Smart Link is not there.
-
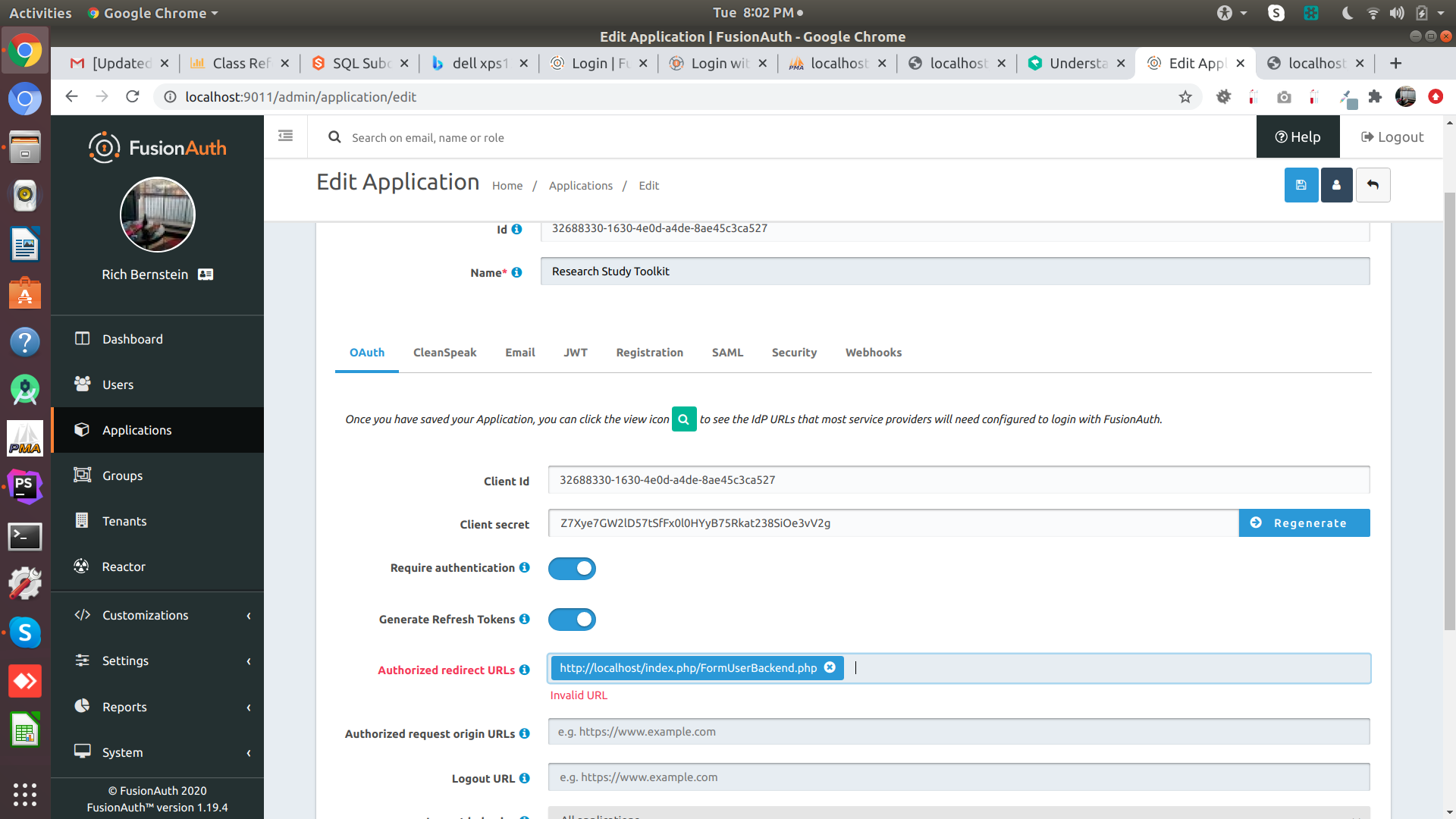
Well I almost got it. Here is the screenshot. Notice the invalid URL? I do not have a an SSL Certificate for this laptop. Could this be the issue?
-
Glad to see you're figuring things out.
https/http shouldn't be a problem. Is there a space at the beginning or end of your url?
-
This post is deleted! -
OK. Got it in there.
Now, how should I test that this is working OK? My initial plan was to a) add users via the API b) send login message via email c) have users complete login via link in email d) have user hot the Send button to submit the form.
But now I think i should test step by step. What is next?
-
Heya,
Are you asking for some free consulting
 ?
?I think testing/writing each of these steps separately is a good idea. Step a should be pretty straightforward, step b doesn't involve fusionauth (I don't think, we do have a welcome email, but that happens when you add the user without any action). step c is your code + a fusionauth API call and step d is your code too.
-
Are you asking for some free consulting
 ?
?No, I can play this "trial and error" game for months :). Seriously though, I am a little concerned that I couldn't enter the URL for quite a few days and then it started working. I just want to be sure that the authorized request origin URL is actually being used. Is there some easy way to test that without using the API?
Did I mention that I appreciate your help and the T-shirt too? -
Sounds good

If you want to verify it is working:
- start up your php app
- add a user in the admin screen
- register the user for your application
- go to the list of applications, click on the green magnifying glass next to your application and look for the 'login url'. copy that.
- open an incognito window
- paste the url
- you should be prompted to login. use the username and password of the user you just added
- you should end up at the redirect URL
for what to do from there, I'd suggest looking at this code: https://github.com/FusionAuth/fusionauth-example-php-connector/blob/auth-with-oauth/oauth-callback.php#L24 which gets a token.
You could also start making API calls, as shown in this code: https://github.com/FusionAuth/fusionauth-example-php-webhook/blob/master/webhook.php#L36 (you won't want to make that call, but that's how you'd initialize a client and make calls to, say, update the user's data.
-
OK Dan. I have gotten the email sent and I do show up at the redirect URL. Now I need to get the access token. To do this I need the $provider, which you can see depends on the $clientId and $clientSecret (see below). But if I put these in the application, won't this be a security problem?
$provider = new \League\OAuth2\Client\Provider\GenericProvider([
'clientId' => $client_id,
'clientSecret' => $client_secret,
'redirectUri' => $redirect_uri,
'urlAuthorize' => $fa_url.'/oauth2/authorize',
'urlAccessToken' => $fa_url.'/oauth2/token',
'urlResourceOwnerDetails' => $fa_url.'/oauth2/userinfo'
]);So my question is how do I get an access token inside the redirect URL?
-
But if I put these in the application, won't this be a security problem?
If you put them in a javascript app, yes. But if they are in the php application only, then it'll be like a database password. Not really a security issue.
You could also inject them as an environment variable or pull from a secrets manager; however you manage your database credentials, I'd suggest doing the same with the client id/secret.